Ctrl+K

Biomass, synthetic fuels and carbon management

Note

You can download this example as a Jupyter notebook or start it in interactive mode.

Biomass, synthetic fuels and carbon management#

In this example we show how to manage different biomass stocks with different potentials and costs, synthetic fuel production, direct air capture (DAC) and carbon capture and usage/sequestration/cycling (CCU/S/C).

Demand for electricity and diesel transport have to be met from various biomass sources, natural gas with possibility for carbon capture, electrolysis for hydrogen production, direct air capture of CO2, and diesel synthesis via Fischer-Tropsch.

The system has to reach a target of net negative emissions over the period.

All numbers/costs/efficiencies are fictitious to allow easy analysis.

[1]:

import pypsa
import numpy as np
import matplotlib.pyplot as plt

ERROR 1: PROJ: proj_create_from_database: Open of /home/docs/checkouts/readthedocs.org/user_builds/pypsa/conda/latest/share/proj failed

[2]:

n = pypsa.Network()
n.set_snapshots(range(10))

Add a constant electrical load

[3]:

n.add("Bus", "bus")
n.add("Load", "load", bus="bus", p_set=1.0)

Add a constant demand for transport

[4]:

n.add("Bus", "transport")
n.add("Load", "transport", bus="transport", p_set=1.0)


n.add("Bus", "diesel")


n.add("Store", "diesel", bus="diesel", e_cyclic=True, e_nom=1000.0)

Add a bus for Hydrogen storage.

[5]:

n.add("Bus", "hydrogen")

n.add("Store", "hydrogen", bus="hydrogen", e_cyclic=True, e_nom=1000.0)

# n.add("Load","hydrogen",
#      bus="hydrogen",
#      p_set=1.)

n.add("Link", "electrolysis", p_nom=2.0, efficiency=0.8, bus0="bus", bus1="hydrogen")

Allow production of diesel from H2 and CO2 using Fischer-Tropsch

[6]:

n.add(
    "Link",
    "FT",
    p_nom=4,
    bus0="hydrogen",
    bus1="diesel",
    bus2="co2 stored",
    efficiency=1.0,
    efficiency2=-1,
)

# minus sign because opposite to how fossil fuels used:
# CH4 burning puts CH4 down, atmosphere up
n.add("Carrier", "co2", co2_emissions=-1.0)

# this tracks CO2 in the atmosphere
n.add("Bus", "co2 atmosphere", carrier="co2")

# NB: can also be negative
n.add("Store", "co2 atmosphere", e_nom=1000, e_min_pu=-1, bus="co2 atmosphere")

# this tracks CO2 stored, e.g. underground
n.add("Bus", "co2 stored")

# NB: can also be negative
n.add("Store", "co2 stored", e_nom=1000, e_min_pu=-1, bus="co2 stored")

Direct air capture consumes electricity to take CO2 from the air to the underground store

[7]:

n.add(
    "Link",
    "DAC",
    bus0="bus",
    bus1="co2 stored",
    bus2="co2 atmosphere",
    efficiency=1,
    efficiency2=-1,
    p_nom=5.0,
)

Meet transport with diesel

[8]:

n.add(
    "Link",
    "diesel car",
    bus0="diesel",
    bus1="transport",
    bus2="co2 atmosphere",
    efficiency=1.0,
    efficiency2=1.0,
    p_nom=2.0,
)

n.add("Bus", "gas")

n.add("Store", "gas", e_initial=50, e_nom=50, marginal_cost=20, bus="gas")

n.add(
    "Link",
    "OCGT",
    bus0="gas",
    bus1="bus",
    bus2="co2 atmosphere",
    p_nom_extendable=True,
    efficiency=0.5,
    efficiency2=1,
)


n.add(
    "Link",
    "OCGT+CCS",
    bus0="gas",
    bus1="bus",
    bus2="co2 stored",
    bus3="co2 atmosphere",
    p_nom_extendable=True,
    efficiency=0.4,
    efficiency2=0.9,
    efficiency3=0.1,
)

Add a cheap and a expensive biomass generator.

[9]:

biomass_marginal_cost = [20.0, 50.0]
biomass_stored = [40.0, 15.0]

for i in range(2):
    n.add("Bus", "biomass" + str(i))

    n.add(
        "Store",
        "biomass" + str(i),
        bus="biomass" + str(i),
        e_nom_extendable=True,
        marginal_cost=biomass_marginal_cost[i],
        e_nom=biomass_stored[i],
        e_initial=biomass_stored[i],
    )

    # simultaneously empties and refills co2 atmosphere
    n.add(
        "Link",
        "biomass" + str(i),
        bus0="biomass" + str(i),
        bus1="bus",
        p_nom_extendable=True,
        efficiency=0.5,
    )

    n.add(
        "Link",
        "biomass+CCS" + str(i),
        bus0="biomass" + str(i),
        bus1="bus",
        bus2="co2 stored",
        bus3="co2 atmosphere",
        p_nom_extendable=True,
        efficiency=0.4,
        efficiency2=1.0,
        efficiency3=-1,
    )


# can go to -50, but at some point can't generate enough electricity for DAC and demand
target = -50

Add a global CO\(_2\) constraint.

[10]:

n.add(
    "GlobalConstraint",
    "co2_limit",
    sense="<=",
    carrier_attribute="co2_emissions",
    constant=target,
)

[11]:

n.optimize();

WARNING:pypsa.components:The following links have bus2 which are not defined:
Index(['electrolysis'], dtype='object', name='Link')

WARNING:pypsa.components:The following links have bus3 which are not defined:
Index(['electrolysis', 'FT', 'DAC', 'diesel car', 'OCGT'], dtype='object', name='Link')

WARNING:pypsa.components:The following links have bus2 which are not defined:
Index(['electrolysis'], dtype='object', name='Link')

WARNING:pypsa.components:The following links have bus3 which are not defined:
Index(['electrolysis', 'FT', 'DAC', 'diesel car', 'OCGT'], dtype='object', name='Link')

INFO:linopy.model: Solve problem using Glpk solver

INFO:linopy.io: Writing time: 0.06s

INFO:linopy.solvers:GLPSOL--GLPK LP/MIP Solver 5.0
Parameter(s) specified in the command line:
 --lp /tmp/linopy-problem-drv671tj.lp --output /tmp/linopy-solve-iavql4_b.sol
Reading problem data from '/tmp/linopy-problem-drv671tj.lp'...
509 rows, 248 columns, 1004 non-zeros
2809 lines were read
GLPK Simplex Optimizer 5.0
509 rows, 248 columns, 1004 non-zeros
Preprocessing...
230 rows, 235 columns, 702 non-zeros
Scaling...
 A: min|aij| =  1.000e-01  max|aij| =  1.000e+00  ratio =  1.000e+01
Problem data seem to be well scaled
Constructing initial basis...
Size of triangular part is 228
      0: obj =   0.000000000e+00 inf =   7.028e+02 (49)
     88: obj =   1.916666667e+03 inf =   3.480e-15 (0)
*    92: obj =   1.916666667e+03 inf =   2.865e-15 (0)
OPTIMAL LP SOLUTION FOUND
Time used:   0.0 secs
Memory used: 0.5 Mb (482195 bytes)
Writing basic solution to '/tmp/linopy-solve-iavql4_b.sol'...


INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 248 primals, 509 duals
Objective: 1.92e+03
Solver model: not available
Solver message: optimal


/home/docs/checkouts/readthedocs.org/user_builds/pypsa/conda/latest/lib/python3.11/site-packages/pypsa/optimization/optimize.py:357: FutureWarning: A value is trying to be set on a copy of a DataFrame or Series through chained assignment using an inplace method.
The behavior will change in pandas 3.0. This inplace method will never work because the intermediate object on which we are setting values always behaves as a copy.

For example, when doing 'df[col].method(value, inplace=True)', try using 'df.method({col: value}, inplace=True)' or df[col] = df[col].method(value) instead, to perform the operation inplace on the original object.


  n.df(c)[attr + "_opt"].update(df)
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Link-fix-p-lower, Link-fix-p-upper, Link-ext-p-lower, Link-ext-p-upper, Store-fix-e-lower, Store-fix-e-upper, Store-ext-e-lower, Store-ext-e-upper, Store-energy_balance were not assigned to the network.

How do the different stores in the system behave?

[12]:

n.stores_t.e.plot(figsize=(9, 7), lw=3)
plt.tight_layout()
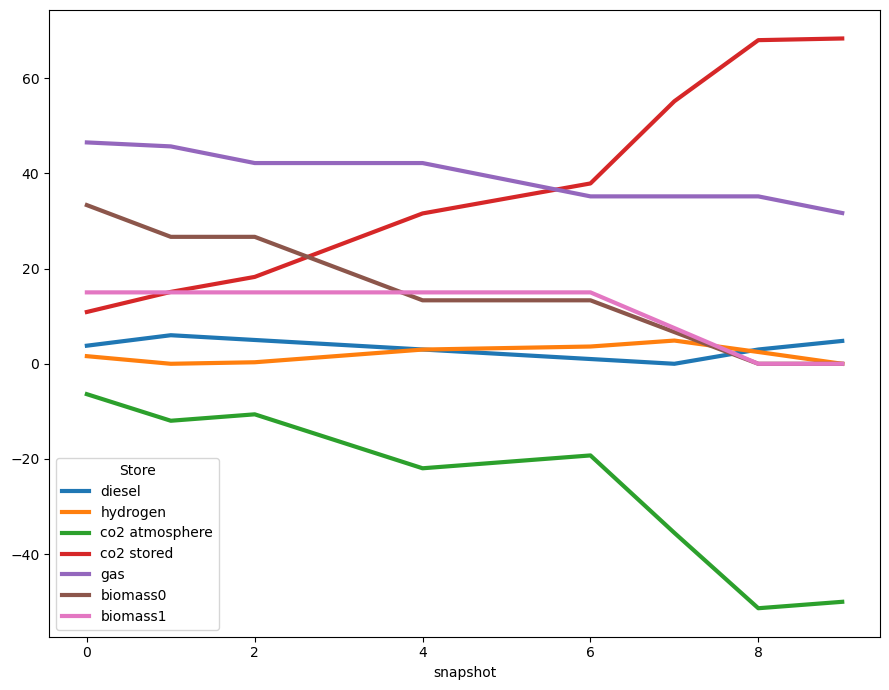
../_images/examples_biomass-synthetic-fuels-carbon-management_21_0.png

Let’s have a look at the production

[13]:

n.links_t.p0[["biomass+CCS0", "biomass+CCS1", "OCGT+CCS", "DAC"]].plot(
    subplots=True, figsize=(9, 7)
)
plt.tight_layout()
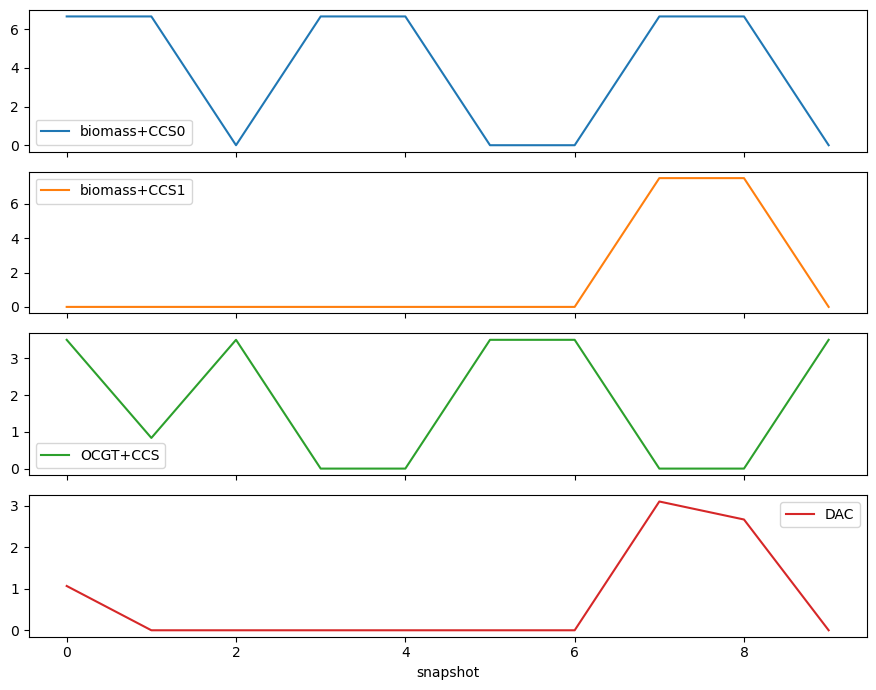
../_images/examples_biomass-synthetic-fuels-carbon-management_23_0.png

At all times, the amount of carbon is constant!

[14]:

n.stores_t.e[["co2 stored", "co2 atmosphere", "gas", "diesel"]].sum(axis=1)

[14]:

snapshot
0    54.79997
1    54.80000
2    54.80000
3    54.80010
4    54.80000
5    54.80000
6    54.80000
7    54.80000
8    54.80000
9    54.80000
dtype: float64