Note

You can download this example as a Jupyter notebook or start it in interactive mode.

Using the statistics module in PyPSA#

The statistics module is used to easily extract information from your networks. This is useful when inspecting your solved networks and creating first visualizations of your results.

With the statistics module, you can look at different metrics of your network. A list of the implemented metrics are:

Capital expenditure
Operational expenditure
Installed capacities
Optimal capacities
Supply
Withdrawal
Curtailment
Capacity Factor
Revenue
Market value
Energy balance

Now lets look at an example.

[1]:

import matplotlib.pyplot as plt
import numpy as np

import pypsa

First, we open an example network we want to investigate.

[2]:

n = pypsa.examples.scigrid_de()

WARNING:pypsa.io:Importing network from PyPSA version v0.17.1 while current version is v0.32.0. Read the release notes at https://pypsa.readthedocs.io/en/latest/release_notes.html to prepare your network for import.
INFO:pypsa.io:Imported network scigrid-de.nc has buses, generators, lines, loads, storage_units, transformers

Lets run an overview of all statistics by calling:

[3]:

n.statistics().dropna()

[3]:

		Installed Capacity
Generator	Brown Coal	20879.50000
	Gas	23913.13000
	Geothermal	31.70000
	Hard Coal	25312.60000
	Multiple	152.70000
	Nuclear	12068.00000
	Oil	2710.20000
	Other	3027.80000
	Run of River	3999.10000
	Solar	37041.52478
	Storage Hydro	1445.00000
	Waste	1645.90000
	Wind Offshore	2973.50000
	Wind Onshore	37339.89533
Line	-	961101.13671
StorageUnit	Pumped Hydro	9179.50000
Transformer	-	192000.00000

So far the statistics are not so interesting, because we have not solved the network yet. We can only see that the network already has some installed capacities for different components.

You can see that statistics returns a pandas.DataFrame. The MultiIndex of the DataFrame provides the name of the network component (i.e. first entry of the MultiIndex, like Generator, Line,…) on the first index level. The carrier index level provides the carrier name of the given component. For example, in n.generators, we have the carriers Brown Coal, Gas and so on.

Now lets solve the network.

[4]:

n.optimize(n.snapshots[:4])

WARNING:pypsa.consistency:The following transformers have zero r, which could break the linear load flow:
Index(['2', '5', '10', '12', '13', '15', '18', '20', '22', '24', '26', '30',
       '32', '37', '42', '46', '52', '56', '61', '68', '69', '74', '78', '86',
       '87', '94', '95', '96', '99', '100', '104', '105', '106', '107', '117',
       '120', '123', '124', '125', '128', '129', '138', '143', '156', '157',
       '159', '160', '165', '184', '191', '195', '201', '220', '231', '232',
       '233', '236', '247', '248', '250', '251', '252', '261', '263', '264',
       '267', '272', '279', '281', '282', '292', '303', '307', '308', '312',
       '315', '317', '322', '332', '334', '336', '338', '351', '353', '360',
       '362', '382', '384', '385', '391', '403', '404', '413', '421', '450',
       '458'],
      dtype='object', name='Transformer')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.19s

Running HiGHS 1.9.0 (git hash: fa40bdf): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e-02, 2e+02]
  Cost   [3e+00, 1e+02]
  Bound  [0e+00, 0e+00]
  RHS    [7e-08, 7e+03]
Presolving model
3039 rows, 6678 cols, 18336 nonzeros  0s
2270 rows, 5901 cols, 17204 nonzeros  0s
2039 rows, 5048 cols, 16272 nonzeros  0s
Presolve : Reductions: rows 2039(-21789); columns 5048(-4892); elements 16272(-27634)
Solving the presolved LP
Using EKK dual simplex solver - serial
  Iteration        Objective     Infeasibilities num(sum)
          0     0.0000000000e+00 Ph1: 0(0) 0s
       2530     1.0389598073e+06 Pr: 0(0); Du: 0(6.39488e-14) 0s
Solving the original LP from the solution after postsolve

INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 9940 primals, 23828 duals
Objective: 1.04e+06
Solver model: available
Solver message: optimal

INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper, Transformer-fix-s-lower, Transformer-fix-s-upper, StorageUnit-fix-p_dispatch-lower, StorageUnit-fix-p_dispatch-upper, StorageUnit-fix-p_store-lower, StorageUnit-fix-p_store-upper, StorageUnit-fix-state_of_charge-lower, StorageUnit-fix-state_of_charge-upper, Kirchhoff-Voltage-Law, StorageUnit-energy_balance were not assigned to the network.

Model name          : linopy-problem-o8uf6r_y
Model status        : Optimal
Simplex   iterations: 2530
Objective value     :  1.0389598073e+06
Relative P-D gap    :  5.6585189444e-14
HiGHS run time      :          0.21
Writing the solution to /tmp/linopy-solve-hvjypqyp.sol

[4]:

('ok', 'optimal')

Now we can look at the statistics of the solved network.

[5]:

n.statistics().round(1)

[5]:

		Optimal Capacity	Installed Capacity	Supply	Withdrawal	Energy Balance	Transmission	Capacity Factor	Curtailment	Operational Expenditure	Revenue	Market Value
Generator	Brown Coal	20879.5	20879.5	42859.0	0.0	42859.0	0.0	0.1	458249.0	428590.4	588266.6	13.7
	Gas	23913.1	23913.1	79.4	0.0	79.4	0.0	0.0	573835.7	3971.9	3971.9	50.0
	Geothermal	31.7	31.7	0.0	0.0	0.0	0.0	0.0	760.8	0.0	0.0	0.0
	Hard Coal	25312.6	25312.6	10535.7	0.0	10535.7	0.0	0.0	596966.7	263391.6	272172.0	25.8
	Multiple	152.7	152.7	0.0	0.0	0.0	0.0	0.0	3664.8	0.0	0.0	0.0
	Nuclear	12068.0	12068.0	31473.0	0.0	31473.0	0.0	0.1	258159.0	251783.9	527108.2	16.7
	Oil	2710.2	2710.2	0.0	0.0	0.0	0.0	0.0	65044.8	0.0	0.0	0.0
	Other	3027.8	3027.8	336.0	0.0	336.0	0.0	0.0	72331.2	10752.0	11503.2	34.2
	Run of River	3999.1	3999.1	13723.3	0.0	13723.3	0.0	0.1	82255.1	41170.0	301812.3	22.0
	Solar	37041.5	37041.5	0.0	0.0	0.0	0.0	0.0	47391.0	0.0	0.0	0.0
	Storage Hydro	1445.0	1445.0	3580.0	0.0	3580.0	0.0	0.1	31100.0	10740.0	72904.4	20.4
	Waste	1645.9	1645.9	4760.0	0.0	4760.0	0.0	0.1	34741.6	28560.0	97621.8	20.5
	Wind Offshore	2973.5	2973.5	5197.6	0.0	5197.6	0.0	0.1	64276.1	0.0	14034.2	2.7
	Wind Onshore	37339.9	37339.9	83669.6	0.0	83669.6	0.0	0.1	389770.6	0.0	406030.6	4.9
Line	AC	961101.1	961101.1	840704.9	840704.9	0.0	-15868.5	0.0	0.0	0.0	1045149.1	1.2
Load	-	0.0	0.0	0.0	195357.1	-195357.1	0.0	NaN	0.0	0.0	-3396077.6	NaN
StorageUnit	Pumped Hydro	9179.5	9179.5	0.0	856.6	-856.6	0.0	0.0	221164.6	0.0	4013.3	NaN
Transformer	-	192000.0	192000.0	103490.2	103490.2	0.0	13253.6	0.0	0.0	0.0	51489.9	0.5

As you can see there is now much more information available. There are still no capital expenditures in the network, because we only performed an operational optimization with this example network.

If you are interested in a specific metric, e.g. curtailment, you can run

[6]:

curtailment = n.statistics.curtailment()
curtailment[curtailment != 0]

[6]:

component    carrier
Generator    Brown Coal       458248.95695
             Gas              573835.68199
             Geothermal          760.80000
             Hard Coal        596966.73690
             Multiple           3664.80000
             Nuclear          258159.00702
             Oil               65044.80000
             Other             72331.20000
             Run of River      82255.08175
             Solar             47391.04321
             Storage Hydro     31100.00000
             Waste             34741.60000
             Wind Offshore     64276.06074
             Wind Onshore     389770.62434
StorageUnit  Pumped Hydro     221164.55428
dtype: float64

Note that when calling a specific metric the statistics module returns a pandas.Series. To find the unit of the data returned by statistics, you can call attrs on the DataFrame or Series.

[7]:

curtailment.attrs

[7]:

{'name': 'Curtailment', 'unit': 'MWh'}

So the unit of curtailment is given in MWh. You can also customize your request.

For this you have various options:

You can select the component from which you want to get the metric with the attribute comps. Careful, comps has to be a list of strings.

[8]:

n.statistics.supply(comps=["Generator"])

[8]:

component  carrier
Generator  Brown Coal       42859.04305
           Gas                 79.43801
           Hard Coal        10535.66310
           Nuclear          31472.99298
           Other              336.00000
           Run of River     13723.31825
           Storage Hydro     3580.00000
           Waste             4760.00000
           Wind Offshore     5197.58856
           Wind Onshore     83669.63033
Name: generators, dtype: float64

For metrics which have a time dimension, you can choose the aggregation method or decide to not aggregate them at all. Just use the aggregate_time attribute to specify what you want to do.

For example calculate the mean supply/generation per time step is

[9]:

n.statistics.supply(comps=["Generator"], aggregate_time="mean")

[9]:

component  carrier
Generator  Brown Coal       1785.79346
           Gas                 3.30992
           Hard Coal         438.98596
           Nuclear          1311.37471
           Other              14.00000
           Run of River      571.80493
           Storage Hydro     149.16667
           Waste             198.33333
           Wind Offshore     216.56619
           Wind Onshore     3486.23460
Name: generators, dtype: float64

Or retrieve the supply time series by not aggregating the time series.

[10]:

n.statistics.supply(comps=["Generator"], aggregate_time=False).iloc[:, :4]

[10]:

	snapshot	2011-01-01 00:00:00	2011-01-01 01:00:00	2011-01-01 02:00:00	2011-01-01 03:00:00
component	carrier
Generator	Brown Coal	12563.90542	10848.56570	10006.39257	9440.17936
	Gas	35.82685	23.72173	13.08297	6.80647
	Geothermal	NaN	NaN	NaN	NaN
	Hard Coal	4778.48239	3124.54667	1722.86855	909.76549
	Multiple	NaN	NaN	NaN	NaN
	Nuclear	7842.04133	7863.18488	7882.53203	7885.23474
	Oil	NaN	NaN	NaN	NaN
	Other	84.00000	84.00000	84.00000	84.00000
	Run of River	3458.90901	3419.33284	3413.46575	3431.61064
	Solar	NaN	NaN	NaN	NaN
	Storage Hydro	895.00000	895.00000	895.00000	895.00000
	Waste	1167.50000	1240.50000	1184.50000	1167.50000
	Wind Offshore	2259.64928	980.56167	979.11542	978.26219
	Wind Onshore	18868.02000	21284.00651	21640.38271	21877.22112

You can choose how you want to group the components of the network and how to aggregate the groups. By default the components are grouped by their carriers and summed. However, you can change this by providing different groupby and aggregate_groups attributes.

[11]:

n.statistics.supply(comps=["Generator"], groupby=["bus"], aggregate_groups="max")

[11]:

component  bus
Generator  101          1392.59019
           102           970.75000
           103             0.12708
           104_220kV       0.89698
           105_220kV      76.95579
                           ...
           94_220kV      164.61490
           95_220kV      186.42929
           96_220kV       53.03276
           97              0.00251
           98            335.60373
Name: generators, Length: 433, dtype: float64

Now you obtained the maximal supply in one time step for every bus in the network.

The keys in the provided in the groupby argument is primarily referring to grouper functions registered in the n.statistics.grouper class. You can also provide a custom function to group the components. Let’s say you want to group the components by the carrier and the price zone. The carrier grouping is already implemented in the grouper class, but the price zone grouping is not. You can provide a custom function to group the components by the price zone.

[12]:

# Create random number generator
rng = np.random.default_rng()

# Use new Generator API
n.buses["price_zone"] = rng.choice(
    [1, 2, 3, 4], size=n.buses.shape[0]
)  # add random price zones


def get_price_zone(n, c, port):
    bus = f"bus{port}"
    return n.static(c)[bus].map(n.buses.price_zone).rename("price_zone")


n.statistics.groupers.register_grouper("price_zone", get_price_zone)

n.statistics.supply(
    comps=["Generator"], groupby=["carrier", "price_zone"], aggregate_groups="sum"
)

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
Cell In[12], line 15
     11     bus = f"bus{port}"
     12     return n.static(c)[bus].map(n.buses.price_zone).rename("price_zone")
---> 15 n.statistics.groupers.register_grouper("price_zone", get_price_zone)
     17 n.statistics.supply(
     18     comps=["Generator"], groupby=["carrier", "price_zone"], aggregate_groups="sum"
     19 )

AttributeError: 'DeprecatedGroupers' object has no attribute 'register_grouper'

Often it is better when inspecting your network to visualize the tables. Therefore, you can easily make plots to analyze your results. For example the supply of the generators.

[13]:

n.statistics.supply(comps=["Generator"]).droplevel(0).div(1e3).plot.bar(
    title="Generator in GWh"
)

[13]:

<Axes: title={'center': 'Generator in GWh'}, xlabel='carrier'>

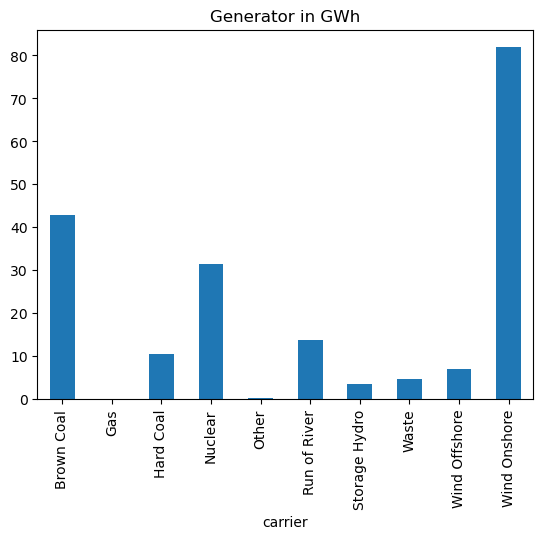
Or you could plot the generation time series of the generators.

[14]:

fig, ax = plt.subplots()
n.statistics.supply(comps=["Generator"], aggregate_time=False).droplevel(0).iloc[
    :, :4
].div(1e3).T.plot.area(
    title="Generation in GW",
    ax=ax,
    legend=False,
    linewidth=0,
)
ax.legend(bbox_to_anchor=(1, 0), loc="lower left", title=None, ncol=1)

[14]:

<matplotlib.legend.Legend at 0x7fc31dac4050>

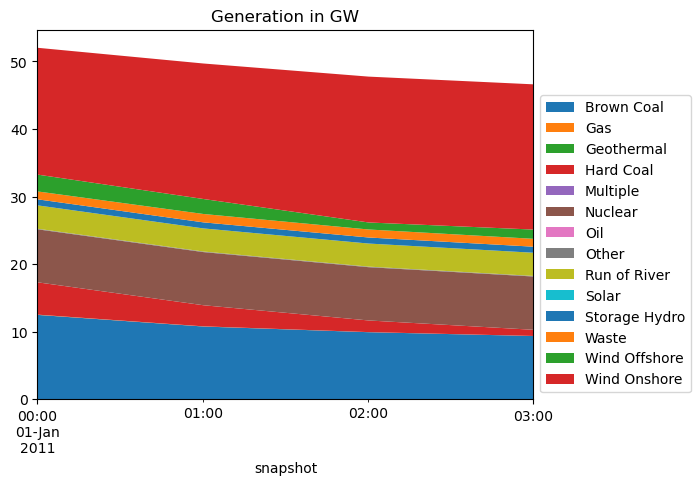
Finally, we want to look at the energy balance of the network. The energy balance is not included in the overview of the statistics module. To calculate the energy balance, you can do

[15]:

n.statistics.energy_balance()

[15]:

component    carrier        bus_carrier
Generator    Brown Coal     AC              42859.04305
             Gas            AC                 79.43801
             Hard Coal      AC              10535.66310
             Nuclear        AC              31472.99298
             Other          AC                336.00000
             Run of River   AC              13723.31825
             Storage Hydro  AC               3580.00000
             Waste          AC               4760.00000
             Wind Offshore  AC               5197.58856
             Wind Onshore   AC              83669.63033
Load         -              AC            -195357.12000
StorageUnit  Pumped Hydro   AC               -856.55428
dtype: float64

Note that there is now an additional index level called bus carrier. This is because an energy balance is defined for every bus carrier. The bus carriers you have in your network you can find by looking at n.buses.carrier.unique(). For this network, there is only one bus carrier which is AC and corresponds to electricity. However, you can have further bus carriers for example when you have a sector coupled network. You could have heat or CO \(_2\) as bus carrier. Therefore, for many statistics functions you have to be careful about the units of the values and it is not always given by the attr object of the DataFrame or Series.

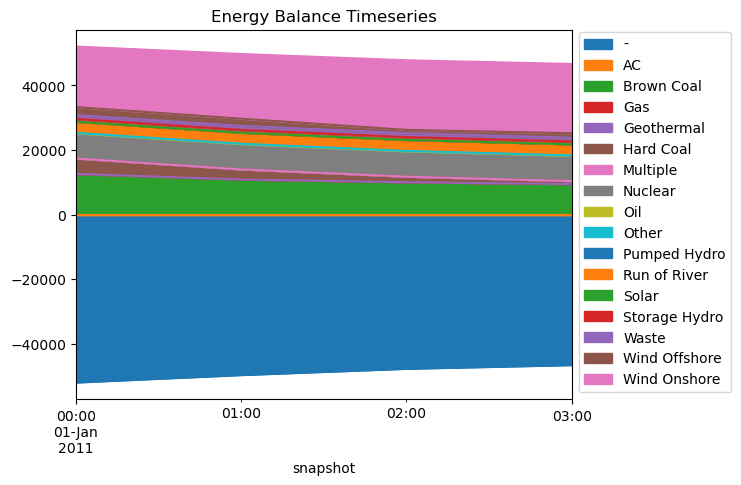
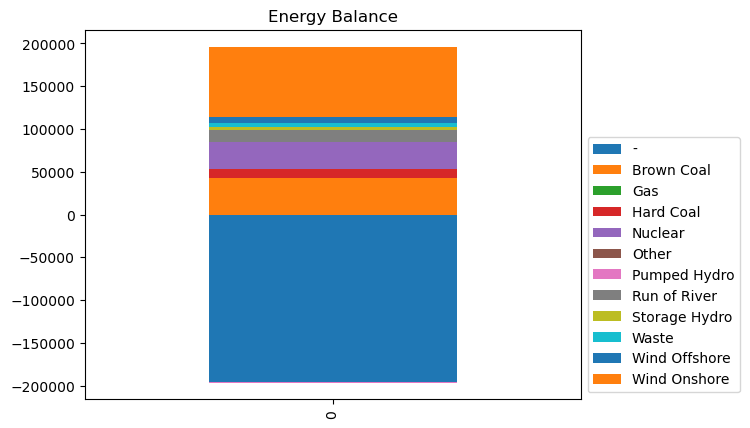
Finally, we want to plot the energy balance and the energy balance time series for electrcity which has the bus carrier AC. In a sector coupled network, you could also choose other bus carriers like H2 or heat. Note that in this example “-” represents the load in the system.

[16]:

fig, ax = plt.subplots()
n.statistics.energy_balance().loc[:, :, "AC"].groupby(
    "carrier"
).sum().to_frame().T.plot.bar(stacked=True, ax=ax, title="Energy Balance")
ax.legend(bbox_to_anchor=(1, 0), loc="lower left", title=None, ncol=1)

[16]:

<matplotlib.legend.Legend at 0x7fc31d9b56d0>

[17]:

fig, ax = plt.subplots()
n.statistics.energy_balance(aggregate_time=False).loc[:, :, "AC"].droplevel(0).iloc[
    :, :4
].groupby("carrier").sum().where(lambda x: np.abs(x) > 1).fillna(0).T.plot.area(
    ax=ax, title="Energy Balance Timeseries"
)
ax.legend(bbox_to_anchor=(1, 0), loc="lower left", title=None, ncol=1)

[17]:

<matplotlib.legend.Legend at 0x7fc31f975810>