Power Flow#
Full non-linear power flow#
The non-linear power flow network.pf() works for AC networks and
by extension for DC networks too (with a work-around described below).
The non-linear power flow network.pf() can be called for a
particular snapshot as network.pf(snapshot) or on an iterable
of snapshots as network.pf(snapshots) to calculate the
non-linear power flow on a selection of snapshots at once (which is
more performant than calling network.pf on each snapshot
separately). If no argument is passed, it will be called on all
network.snapshots, see pypsa.Network.pf() for details.
Non-linear power flow for AC networks#
The power flow ensures for given inputs (load and power plant dispatch) that the following equation is satisfied for each bus \(i\):
where \(V_i = |V_i|e^{j\theta_i}\) is the complex voltage, whose rotating angle is taken relative to the slack bus.
\(Y_{ij}\) is the bus admittance matrix, based on the branch impedances and any shunt admittances attached to the buses.
For the slack bus \(i=0\) it is assumed \(|V_0|\) is given and that \(\theta_0 = 0\); P and Q are to be found.
For the PV buses, P and \(|V|\) are given; Q and \(\theta\) are to be found.
For the PQ buses, P and Q are given; \(|V|\) and \(\theta\) are to be found.
If PV and PQ are the sets of buses, then there are \(|PV| + 2|PQ|\) real equations to solve:
To be found: \(\theta_i \forall i \in PV \cup PQ\) and \(|V_i| \forall i \in PQ\).
These equations \(f(x) = 0\) are solved using the Newton-Raphson method, with the Jacobian:
and the initial “flat” guess of \(\theta_i = 0\) and \(|V_i| = 1\) for unknown quantities.
Non-linear power flow for AC networks with distributed slack#
If the slack is to be distributed to all generators in proportion
to their dispatch (distribute_slack=True), instead of being
allocated fully to the slack bus, the active power balance is altered to
where \(P_{slack}\) is the total slack power and \(\gamma_{i}\) is the share of bus \(i\) of the total generation that is used to distribute the slack power. Note that also an additional active power balance is included for the slack bus since it is now part of the distribution scheme.
This adds an additional row to the Jacobian for the derivatives of the slack bus active power balance and an additional column for the partial derivatives with respect to \(\gamma_i\).
Line model#
Lines are modelled with the standard equivalent PI model. In the future a model with distributed parameters may be added.
If the series impedance is given by
and the shunt admittance is given by
then the currents and voltages at buses 0 and 1 for a line:
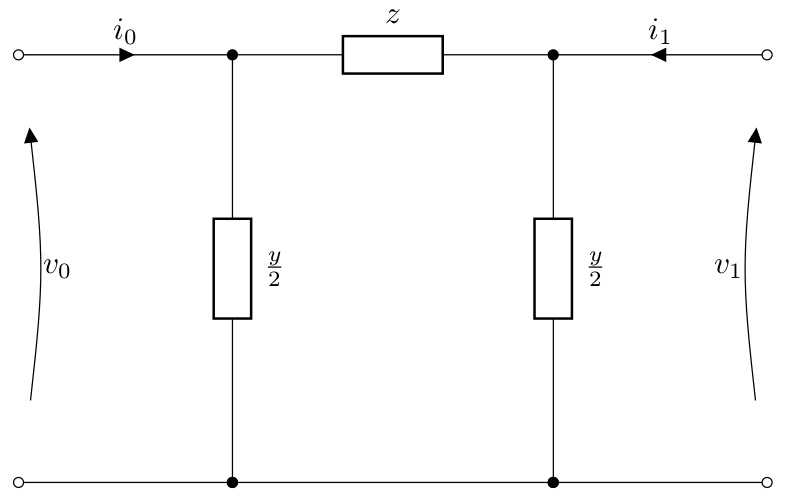
are related by
Transformer model#
The transformer models here are largely based on the implementation in pandapower, which is loosely based on DIgSILENT PowerFactory.
Transformers are modelled either with the equivalent T model (the
default, since this represents the physics better) or with the
equivalent PI model. The can be controlled by setting transformer
attribute model to either t or pi.
The tap changer can either be modelled on the primary, high voltage
side 0 (the default) or on the secondary, low voltage side 1. This is set with attribute tap_side.
If the transformer type is not given, then tap_ratio is
defined by the user, defaulting to 1.. If the type is given,
then the user can specify the tap_position which results in a
tap ratio \(\tau\) given by:
For a transformer with tap ratio \(\tau\) on the primary side
tap_side = 0 and phase shift \(\theta_{\textrm{shift}}\), the
equivalent T model is given by:
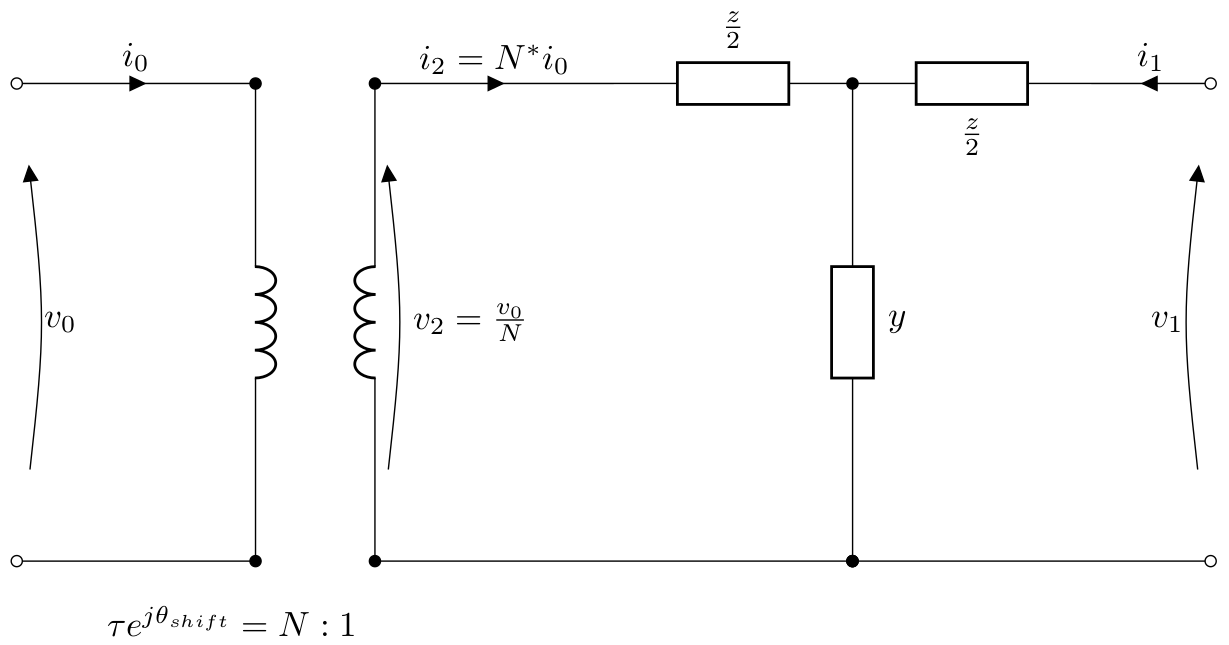
For a transformer with tap ratio \(\tau\) on the secondary side
tap_side = 1 and phase shift \(\theta_{\textrm{shift}}\), the
equivalent T model is given by:
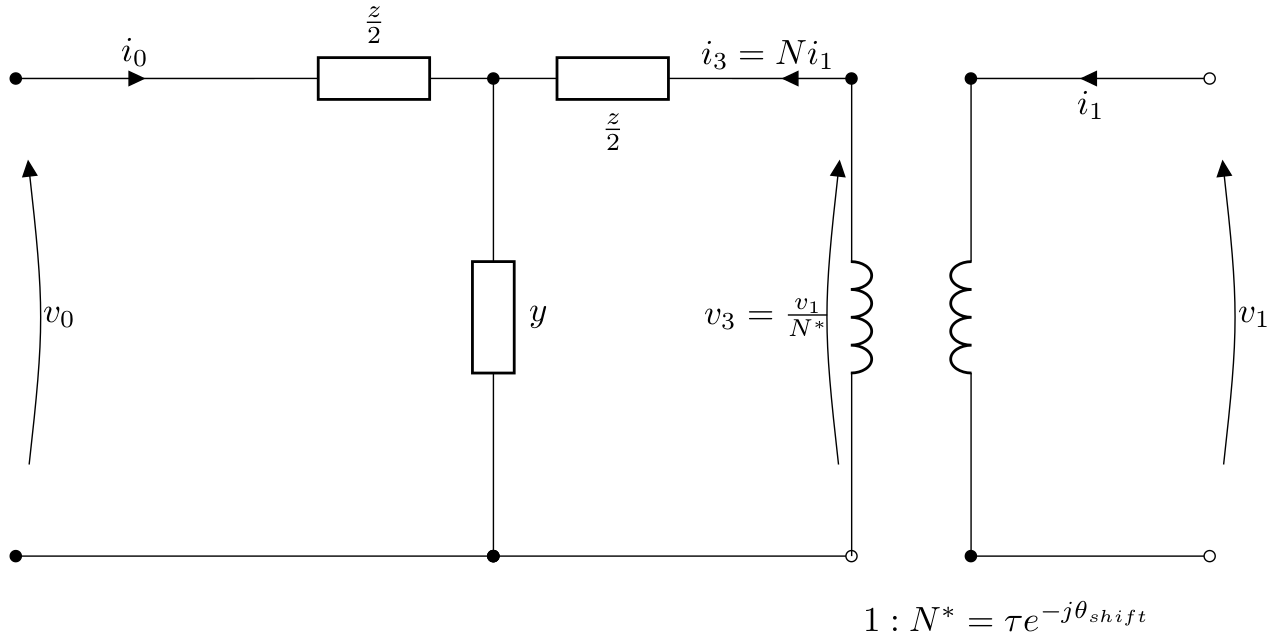
For the admittance matrix, the T model is transformed into a PI model with the wye-delta transformation.
For a transformer with tap ratio \(\tau\) on the primary side
tap_side = 0 and phase shift \(\theta_{\textrm{shift}}\), the
equivalent PI model is given by:
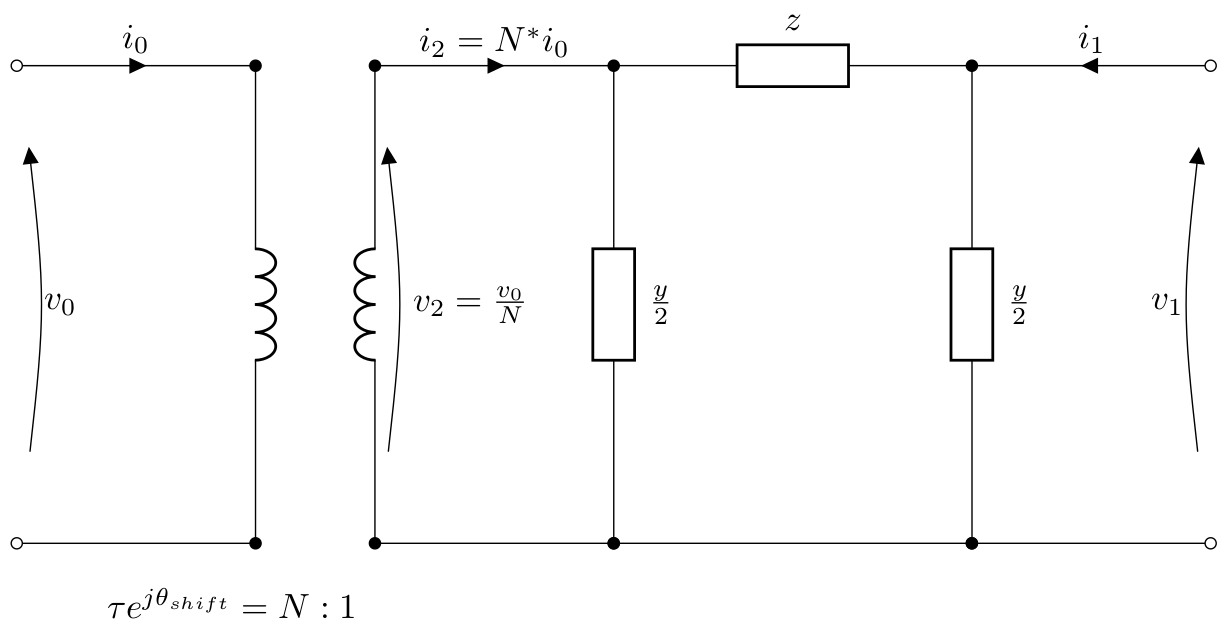
for which the currents and voltages are related by:
For a transformer with tap ratio \(\tau\) on the secondary side
tap_side = 1 and phase shift \(\theta_{\textrm{shift}}\), the
equivalent PI model is given by:
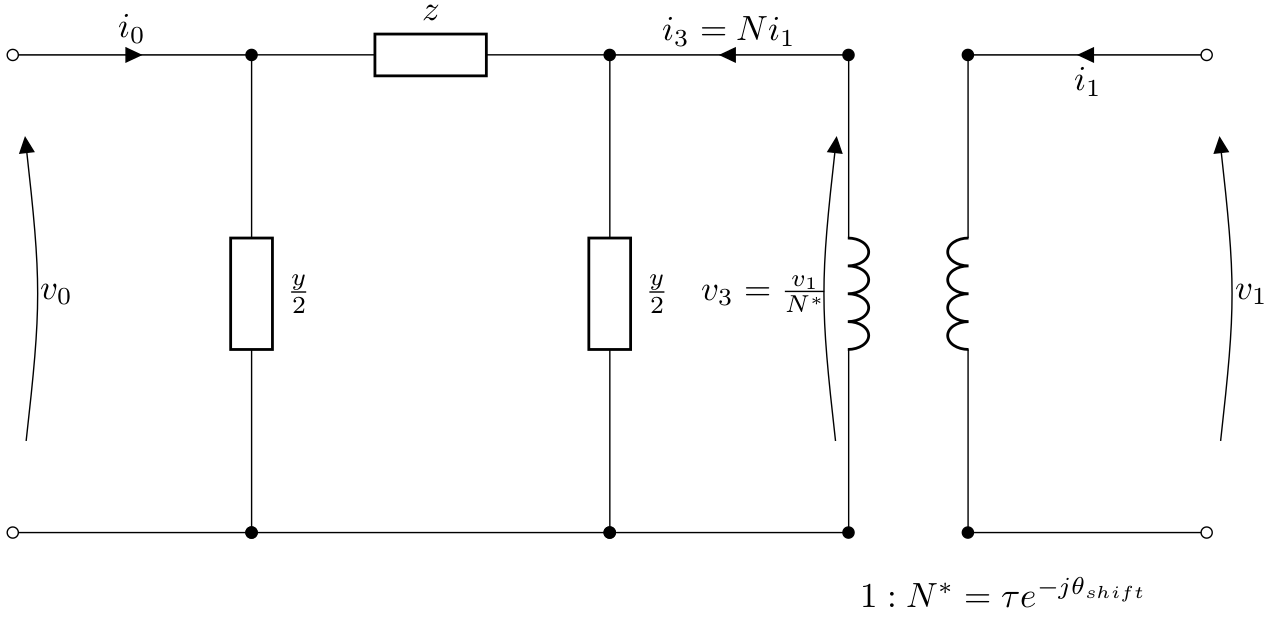
for which the currents and voltages are related by:
Non-linear power flow for DC networks#
For meshed DC networks the equations are a special case of those for AC networks, with the difference that all quantities are real.
To solve the non-linear equations for a DC network, ensure that the
series reactance \(x\) and shunt susceptance \(b\) are zero
for all branches, pick a Slack bus (where \(V_0 = 1\)) and set all
other buses to be ‘PQ’ buses. Then execute network.pf().
The voltage magnitudes then satisfy at each bus \(i\):
where all quantities are real.
\(G_{ij}\) is based only on the branch resistances and any shunt conductances attached to the buses.
Inputs#
For the non-linear power flow, the following data for each component are used. For almost all values, defaults are assumed if not explicitly set. For the defaults and units, see Components.
buses.{v_nom, v_mag_pu_set (if PV generators are attached)}
loads.{p_set, q_set}
generators.{control, p_set, q_set (for control PQ)}
storage_units.{control, p_set, q_set (for control PQ)}
stores.{p_set, q_set}
shunt_impedances.{b, g}
lines.{x, r, b, g}
transformers.{x, r, b, g}
links.{p_set}
Note
Note that the control strategy for active and reactive power PQ/PV/Slack is set on the generators NOT on the buses. Buses then inherit the control strategy from the generators attached at the bus (defaulting to PQ if there is no generator attached). Any PV generator will make the whole bus a PV bus. For PV buses, the voltage magnitude set point is set on the bus, not the generator, with bus.v_mag_pu_set since it is a bus property.
Note
Note that for lines and transformers you MUST make sure that \(r+jx\) is non-zero, otherwise the bus admittance matrix will be singular.
Outputs#
buses.{v_mag_pu, v_ang, p, q}
loads.{p, q}
generators.{p, q}
storage_units.{p, q}
stores.{p, q}
shunt_impedances.{p, q}
lines.{p0, q0, p1, q1}
transformers.{p0, q0, p1, q1}
links.{p0, p1}
Linear power flow#
The linear power flow network.lpf() can be called for a
particular snapshot as network.lpf(snapshot) or on an iterable
of snapshots as network.lpf(snapshots) to calculate the
linear power flow on a selection of snapshots at once (which is
more performant than calling network.lpf on each snapshot
separately). If no argument is passed, it will be called on all
network.snapshots, , see pypsa.Network.lpf() for details.
For AC networks, it is assumed for the linear power flow that reactive power decouples, there are no voltage magnitude variations, voltage angles differences across branches are small and branch resistances are much smaller than branch reactances (i.e. it is good for overhead transmission lines).
For AC networks, the linear load flow is calculated using small voltage angle differences and the series reactances alone.
It is assumed that the active powers \(P_i\) are given for all buses except the slack bus and the task is to find the voltage angles \(\theta_i\) at all buses except the slack bus, where it is assumed \(\theta_0 = 0\).
To find the voltage angles, the following linear set of equations are solved
where \(K\) is the incidence matrix of the network, \(B\) is the diagonal matrix of inverse branch series reactances \(x_l\) multiplied by the tap ratio \(\tau_l\), i.e. \(B_{ll} = b_l = \frac{1}{x_l\tau_l}\) and \(\theta_l^{\textrm{shift}}\) is the phase shift for a transformer. The matrix \(KBK^T\) is singular with a single zero eigenvalue for a connected network, therefore the row and column corresponding to the slack bus is deleted before inverting.
The flows p0 in the network branches at bus0 can then be found by multiplying by the transpose incidence matrix and inverse series reactances:
For DC networks, it is assumed for the linear power flow that voltage magnitude differences across branches are all small.
For DC networks, the linear load flow is calculated using small voltage magnitude differences and series resistances alone.
The linear load flow for DC networks follows the same calculation as for AC networks, but replacing the voltage angles by the difference in voltage magnitude \(\delta V_{n,t}\) and the series reactance by the series resistance \(r_l\).
Inputs#
For the linear power flow, the following data for each component are used. For almost all values, defaults are assumed if not explicitly set. For the defaults and units, see Components.
buses.{v_nom}
loads.{p_set}
generators.{p_set}
storage_units.{p_set}
stores.{p_set}
shunt_impedances.{g}
lines.{x}
transformers.{x}
links.{p_set}
Note
Note that for lines and transformers you MUST make sure that \(x\) is non-zero, otherwise the bus admittance matrix will be singular.
Outputs#
buses.{v_mag_pu, v_ang, p}
loads.{p}
generators.{p}
storage_units.{p}
stores.{p}
shunt_impedances.{p}
lines.{p0, p1}
transformers.{p0, p1}
links.{p0, p1}